1232.缀点成线

(Updated: )
LeetCode
, ,

Q

在一个 XY 坐标系中有一些点，我们用数组 coordinates 来分别记录它们的坐标，其中 coordinates[i] = [x, y] 表示横坐标为 x、纵坐标为 y 的点。

请你来判断，这些点是否在该坐标系中属于同一条直线上，是则返回 true，否则请返回 false。

示例 1：

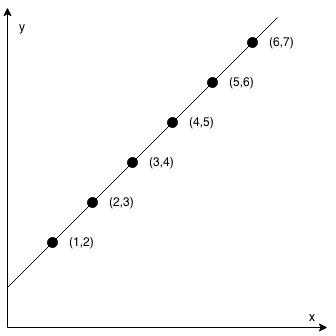
输入：coordinates = [[1,2],[2,3],[3,4],[4,5],[5,6],[6,7]]
输出：true

示例 2：

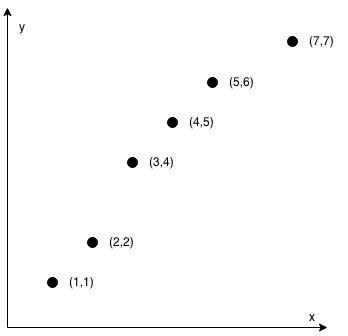
输入：coordinates = [[1,1],[2,2],[3,4],[4,5],[5,6],[7,7]]
输出：false

A

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {     
    public boolean checkStraightLine(int[][] coordinates) {
        for(int i = 1; i < coordinates.length - 1; i++){
            int res1 = (coordinates[i][0] - coordinates[i - 1][0]) * (coordinates[i + 1][1] - coordinates[i][1]);
            int res2 = (coordinates[i + 1][0] - coordinates[i][0]) * (coordinates[i][1] - coordinates[i - 1][1]);
            if(res1 != res2){
                return false;
            }
        }
        return true;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public boolean checkStraightLine(int[][] coordinates) {
        int deltaX = coordinates[0][0], deltaY = coordinates[0][1];
        int n = coordinates.length;
        for (int i = 0; i < n; i++) {
            coordinates[i][0] -= deltaX;
            coordinates[i][1] -= deltaY;
        }
        int A = coordinates[1][1], B = -coordinates[1][0];
        for (int i = 2; i < n; i++) {
            int x = coordinates[i][0], y = coordinates[i][1];
            if (A * x + B * y != 0) {
                return false;
            }
        }
        return true;
    }
}


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public boolean checkStraightLine(int[][] coordinates) {
        int[][] c = coordinates;            //简便缩写
        if(c == null) return false;         //无任何点时，直线不存在
        if(c.length == 1 || c.length ==2) return true;        //只有一个点或者两个点时直接返回true
        //若在一条直线上，斜率必相等
        //即(y2-y1)/(x2-x1)=(yi-y2)/(xi-x2)
        //当直线平行y轴时有除零风险，固交叉相乘改变为乘法
        //即(y2-y1)(xi-x2)=(yi-y2)(x2-x1)
        for(int i = 2;i < c.length;i++){  
            if((c[1][1]-c[0][1]) * (c[i][0]-c[1][0]) == (c[i][1]-c[1][1]) * (c[1][0]-c[0][0]))
            {
                continue;//斜率匹配，继续循环
            }else{
                return false;//不匹配，不为直线
            }
        }
        return true;//匹配完毕，任意节点斜率符合
    }
}

  • 思路
    由斜率公式得
    (y1-y0)/(x1-x0)=(yi-y0)/(xi-x0)
    防止除0，变换成相乘的形式
    (y1-y0)(xi-x0)==(x1-x0)(yi-y0)

尽量避免 y1-y0/x1-x0等求斜率或者除法比较比值的操作，而换成乘法来比较，例如求y=kx+b的解析式或者题解中的方式，因为乘法的开销远小于除法

  • 时间复杂度：
    O(n)，其中 n 是数组中的元素数量。

  • 空间复杂度
    O(1)